有一个著名的问题叫“三门问题”。这个问题的还有一个别名,叫“蒙蒂霍尔问题”。这个问题源自美国智力竞赛节目主持人蒙蒂·霍尔主持的节目。
为何这个问题如此有名呢?
在这里,我不想用数学、 概率论和贝叶斯定理之类的常用方法,而想用我在KCGI教授的经营学特论决策机制章节中介绍的决策树说明这个问题。
首先,让我们来回顾一下三门问题。
玩家可以看到三道门。其中一道门的后面是玩家可以赢取的奖品,而另外两道门则有一只山羊(这意味着没有奖品且未中奖)。节目的主持人知道每道门后面有什么,而玩家不知道门后面有什么。
在玩家做出第一选择之后,主持人蒙蒂打开另外两道门中的一道门露出山羊。然后,主持人给玩家提供选择权,问其是保留最初的选择还是改选另一道关闭的门。
在这里,我们看到的这个问题不是“概率”,而是“期望值”。
假设免费赠品的汽车的价值为120万日元。
基于以上假设,我们可以绘制出以下决策树。
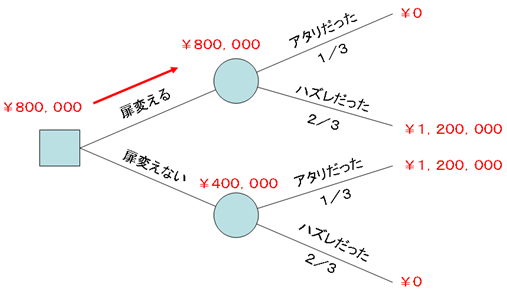
在决策树中,
□是决策节点,表示行动的一个分支。
○是概率节点,表示无法控制的现象。
绘制决策树时,要从左往右进行绘制,写下各节点或分支的状态,然后从右往左寻找最佳决策。
这次,决策节点是:
1.选择哪道门
2.之后,是否要换门
这里有两种类型的决策节点。在这里,我们将选择任何一道门都视为“相同”,并用概率节点表示所选门的“ 概率”。
在左端绘制一个决策节点,并从该节点绘制两个分支,即“换门”和“不换门”。 接下来,从两个概率节点进一步分解成两个分支:“准确”和“不准确”。
根据游戏设置,“最初一击即中”的概率为三分之一,而“从最初就错误”的概率为三分之二。
这里的收益考虑如下。
“准确”→“换门”→变成不准→¥0
“准确”→“不换门”→仍然准确→¥120万
“不准”→“换门”→准确→¥120万
“不准”→→“不换门”→仍然不准→¥0
至此,在我们绘制出决策树后,从右往左进行讨论。
观察“换门”时概率节点(上方)的预期收益:
(¥0*1/3)+(¥1,200,000*2/3)=¥800,000
观察“不换门”时概率节点(下方)的预期收益:
(¥0*2/3)+(¥1,200,000*1/3)=¥400,000
现在,再观察最左边的决策节点。
该决策节点右上分支的预期收益为¥80万,而右下分支的预期收益为¥40万。
由于“¥80万>¥40万”,右上分支即“换门”能够获得更高的预期收益。
因此,在三门问题中,正确的决策是“换门更好”。
这是我们为何学习经营学的原因之一。
李 皓