Hiện đang tồn tại một vấn đề khá nổi tiếng có tên là vấn đề Monty Hall.Hay còn gọi là Monty Hall dilemma.Đây là vấn đề phát sinh từ chương trình mà MC Monty Hall phụ trách trong chương trình đố vui của Mỹ.
Tại sao vấn đề này lại trở nên nổi tiếng,
Ở đây tôi sẽ không dùng những phương pháp như định lý hay học thuyết xác suất thường thấy trong toán học mà tôi muốn giải thích bằng cách sử dụng cây quyết định mà tôi đã giới thiệu trong chương về cơ chế đưa ra quyết định trong bài giảng đặc biệt về quản trị kinh doanh được dạy tại KCGI.
Đầu tiên tôi sẽ nói qua về vấn đề Monty Hall.
Người chơi sẽ được cho nhìn 3 cái cửa.Ở sau 1 cái cửa sẽ có sản phẩm mà người chơi có thể nhận, ở chỗ 2 cái cửa khác sẽ có con dê (không phải là sản phẩm mà nó có nghĩa là đã không trúng).Host của chương trình thì biết là sau mỗi cái cửa sẽ có gì, còn người chơi thì đương nhiên là sẽ không biết.
Sau khi người chơi chọn xong lần 1, Host sẽ mở 1 trong 2 cửa không chứa phần thưởng, sẽ cho thấy con dê.Tại đây Host sẽ cho người chơi quyền lựa chọn, giữ nguyên sự lựa chọn ban đầu, hay thay đổi thành cái cửa đang đóng.
Ở đây ta sẽ thấy được vấn đề là không phải [xác suất] mà sẽ là [Giá trị kỳ vọng].
Giả định giá trị của chiếc Ô-tô phần thưởng là 1.200.000 Yên.
Từ giả định trên ta có thể vẽ được cây quyết định như sau.
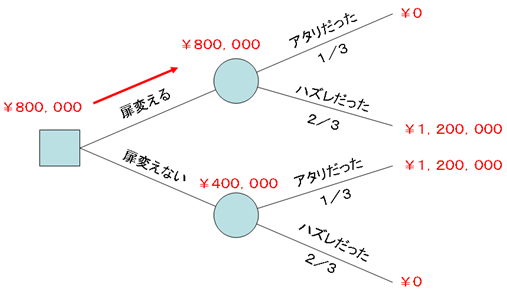
Tại cây quyết định thì,
□ gọi là nút quyết định, thể hiện phân nhánh của hành động.
○ gọi là nút xác suất, thể hiện tình trạng không thể kiểm soát.
Khi vẽ sẽ vẽ từ phải sang trái, vẽ trạng thái các nhánh và các nút, sau đó sẽ tìm quyết định thích hợp nhất từ phải sang trái.
Lần này thì nút quyết định sẽ là:
1Sẽ chọn cánh cửa nào
2Sau đó có đổi cửa hay không
Có 2 lựa chọn như thế, tuy nhiên ở đây tôi đã chọn cách thể hiện là dù có chọn cánh cửa nào đi nữa thì cũng sẽ thể hiện [Xác xuất trúng] của cánh cửa mình đã chọn bằng nút xác suất.
Vẽ nút quyết định ở ngoài cùng bên trái, rồi vẽ 2 nhánh từ nút này, sau đó viết [Đổi cửa], [không đổi cửa]. Sau đó, từ 2 nút xác suất này lại tiếp tục phân 2 nhánh nữa là [trúng] và [trượt].
Từ thiết lập của trò chơi, xác xuất của [trúng ngay từ đầu] là 1/3 và xác suất của [Trượt ngay từ đầu] là 2/3.
Về lợi chúng ta sẽ suy nghĩ như sau.
Đang [Trúng] mà →[đổi cửa] → thành trượt → 0 yên
Đang [Trúng] →[không đổi cửa] →vẫn là trúng →1.200.000 yên
[Trượt] →[Đổi cửa] →Thành [Trúng] →1.200.000 yên
[Trượt] →[Không đổi cửa] →Vẫn là [Trượt] →0 yên
Vẽ cây tới đây ta sẽ xem xét từ phải qua trái.
Thử xem lợi kỳ vọng của nút xác xuất trong trường hợp [Đổi cửa] (phía trên),
(¥0*1/3)+(¥1.200.000*2/3)=¥800.000
Thử xem lợi kỳ vọng của nút xác xuất trong trường hợp [Không đổi cửa] (phía dưới),
(¥0*2/3)+(¥1.200.000*1/3)=¥400.000
Giờ thì nhìn nút quyết định phía ngoài cùng bên trái.
Lợi kỳ vọng của nhánh phía trên bên phải của nút quyết định này sẽ là 800.000 yên, lợi kỳ vọng của nhánh phía dưới bên phải là 400.000 yên.
「¥800.000>¥400.000」nên nhánh trên bên phải, có nghĩa là [đổi cửa] thì sẽ có lợi kỳ vọng cao hơn.
Do đó, với vấn đề Monty Hall quyết định đúng sẽ là [Nên đổi cửa].
Việc này chính là một trong những lý do tại sao chúng ta lại phải học về quản trị kinh doanh.
Lý cảo