There is a famous problem called the Monty Hall problem.Another name for this problem is the “Monty Hall Dilemma”.The problem is derived from an offshoot of a segment featuring the American quiz show hosted by Monty Hall.
Why did it become famous?
After the solution to this problem was discussed in Marilyn vos Savant's "Ask Marilyn" question and answer column in "Parade magazine" in 1990, about 10,000 readers, including several hundred mathematics professors, responded that her answer was wrong (despite the fact that she was actually correct). (Source: http://ja.wikipedia.org/wiki/ Monty Hall Problem )
Here, I would like to explain this problem using the decision tree instead of the usual methods such as common mathematics, probability theory and Bayesian theorem etc. I present the business tree during my lecture on decision making mechanism in “Advanced Topics in Business Administration” course at KCGI,
First, let me review the Monty Hall problem.
The player is shown three doors.Behind one of the doors is a prize that the player can win, while the other two doors contain a goat (meaning that there is no prize and the player has lost).The show host knows what is behind each door, while the player obviously does not know what is behind the door.
After the player makes their first choice, the host, Monty Hall, opens one of the other two doors and shows the goat.The host then gives the player the option to either keep their original selection or change it to for another closed door.Should players change their choice and choose the other door?(Source: http://ja.wikipedia.org/wiki/ Monty Hall Problem )
We look at this problem not as a "probability" but as "expected value".
Let's assume that the value of the prize, a free car is ¥ 1,200,000.
From the above assumptions, the following decision tree can be drawn.
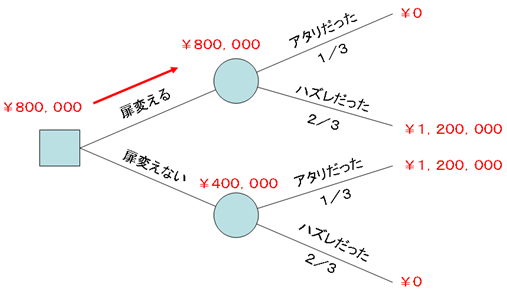
In the decision tree,
□ is a decision node and represents a branch of action.
○ is a probability node and represents an event that cannot be controlled.
When drawing, draw from left to right, write the state of each node and branch, and explore the decision from right to left.
This time, the decision node is:
1.
Which door to choose
2.
Whether or not to change the door
Here, we treat all the doors "equally" and represent the "probability to win" of the selected door as a probability node.
And use one kind of decision node (whether to change the door?)and one type of probability node (does the first choice win?)to draw a decision tree.
Draw a decision node at the left end, and draw two branches from this node: “Change door” and “Do not change door”.Connect both branches to the node that says “Is the current selection winning?"which is the probability node.It then branches from the two probability nodes into two branches, "It won." and "It lost.".
Based on the game settings, the probability of “winning with the fisrt choice ” is one third, and the probability of “losing with the first choice” is two thirds.
This is how we think about the gain.
Even though it was “Correct” → “Change door” → It becomes a loss → ¥ 0
"It was correct"-> "Do not change the door"-> It remains correct-> Keep ¥ 1,200,000 yen
“It was a wrong” → “Change the door” → It became correct → ¥ 1,200,000
Choose the “wrong door” → “Do not change the door” → It still remains incorrect→ ¥ 0
Once you have drawn the tree, consider from the right to left.
Looking at the expected gain of the probability node (upper) in the case of "change door",
(¥ 0 * 1/3) + (¥ 1,200,000 * 2/3) = ¥ 800,000
Looking at the expected gain of the probability node (lower) when the door does not change,
(¥ 0 * 2/3) + (¥ 1,200,000 * 1/3) = ¥ 400,000
Look at the decision node on the far left.
The expected gain of the upper right branch of this decision node is ¥ 800,000, and the expected gain of the lower right branch is ¥ 400,000.
Since “¥ 800,000> ¥ 400,000”, the upper right branch, that is, “change door” has a higher expected gain.
Therefore, the answer to the Monty Hall problem, is that “You should change the door.” This is the right decision.
In this way, when faced with a situation that is difficult to understand intuitively or makes a wrong decision, decision support tools such as decision trees can be used to make better choices.
This is one reason why we study Business Administration.
Lee Hao